Solution pour le challenge 25
Les repunits sont les nombres de la forme :
![Rendered by QuickLaTeX.com \[\boxed{u_{n}=\frac{10^{n}-1}{9}\quad\text{avec }n\in\mathbb{N}^{\star}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3869f88d6274f448aab1013d86ffca0c_l3.png)
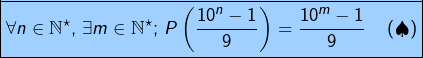
Soit ![]() un tel polynôme et soit
un tel polynôme et soit ![]() défini par
défini par ![]() . Alors :
. Alors :
![]()
![]() n’est donc pas le polynôme nul. Notons
n’est donc pas le polynôme nul. Notons ![]() son degré et
son degré et ![]() son coefficient dominant (
son coefficient dominant (![]() et
et ![]()
On sait que :
![]()
Il s’ensuit que ![]() Et comme
Et comme ![]() il existe
il existe ![]() tel que
tel que ![]()
En outre, 0 étant le seul point d’accumulation de ![]() la suite
la suite ![]() est stationnaire : il existe
est stationnaire : il existe ![]() tel que
tel que
![]()
Comme :
![]()
![]()
Réciproquement, si ![]() est de cette forme, la condition
est de cette forme, la condition ![]() est-elle bien remplie ? Il faut que l’on ait :
est-elle bien remplie ? Il faut que l’on ait :
![]()
![]()
![]()
En conclusion, les polynômes à coefficients réels laissant stable l’ensemble des repunits sont les :![]()
avec ![]() entiers tels que
entiers tels que ![]() et
et ![]() .
.
Pour ![]() et
et ![]() , cette formule donne les polynômes constants solutions (la constante étant évidemment un repunit).
, cette formule donne les polynômes constants solutions (la constante étant évidemment un repunit).
Quelques autres polynômes solutions :
![]() ,
,![]() ,
,![]() ,
,![]()
respectivement obtenus pour :![]() et
et ![]()
![]()
obtenu pour ![]() et
et ![]()
![]()
obtenu pour ![]() et
et ![]()
Tous ces polynômes sont à coefficients rationnels. Et ceux d’entre-eux qui sont à coefficients entiers correspondent à ![]() .
.
Pour consulter l’énoncé, c’est ici

