Solution pour le challenge 21
Si ![]() sont tels que
sont tels que ![]() alors
alors
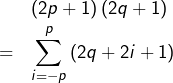
![Rendered by QuickLaTeX.com \[A=\sum_{i=-p}^{p}\left(2q+1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7bbbfcc54baefff8d98f1a877b3d2e96_l3.png)
![Rendered by QuickLaTeX.com \[B=\sum_{i=-p}^{p}2i\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c6f95c8fdace0b107506a67d398aa307_l3.png)
Ceci prouve l’existence d’une telle écriture.
Il n’y a pas unicité, comme on le voit avec l’exemple suivant :
![]()
Maintenant, si ![]() sont deux nombres premiers impairs, l’écriture est unique. En effet, la relation :
sont deux nombres premiers impairs, l’écriture est unique. En effet, la relation :
![Rendered by QuickLaTeX.com \[MN=\sum_{i=m}^{n}\left(2i-1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1dc73ae7da7efa6f22bc4d43ca974382_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left(\star\right)\left\{ \begin{array}{ccc}n-m+1 & = & 1\\\\n+m-1 & = & MN\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6ca11da3a4900eceac2289ecc7c4461f_l3.png)
![Rendered by QuickLaTeX.com \[\left(\star\star\right)\left\{ \begin{array}{ccc}n-m+1 & = & M\\\\n+m-1 & = & N\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c231c6b98f42a1f793ede4fe9a30a36e_l3.png)
La seule possibilité est donc donnée par ![]() , qui entraîne :
, qui entraîne :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}m & = & \frac{N-M+2}{2}\\\\n & = & \frac{N+M}{2}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7eeb962795134dc01442234cb475b570_l3.png)
L’unicité de l’écriture de ![]() comme somme d’entiers impairs consécutifs est établie.
comme somme d’entiers impairs consécutifs est établie.
Pour consulter l’énoncé, c’est ici

