Solution pour le challenge n° 2

Solution pour le challenge 2

Notons $S$ le segment d’extrémités $\left(0,0\right)$ et $\left(p,q\right)$ et notons $d=p\wedge q$ .

Par homogénéité du pgcd, il existe des entiers $P,Q$ premiers entre eux tels que :

$p=Pd\qquad\text{et}\qquad q=Qd$

Notons $S_{x}$ (resp. $S_{y}$ ) l’ensemble des points de $S$ d’abscisse entière (resp. d’ordonnée entière). On cherche $\text{card}\left(S_{x}\cup S_{y}\right)$ .

Il est clair que :

$\begin{eqnarray*}\text{card}\left(S_{x}\right)&=&p+1\\\text{card}\left(S_{y}\right)&=&q+1\end{eqnarray*}$

Par ailleurs $S_{x}\cap S_{y}$ est l’ensemble des points à coordonnées entières de $S$ , à savoir les couples $\left(a,b\right)\in\llbracket0,p\rrbracket\times\llbracket0,q\rrbracket$ tels que $pb=qa$ , c’est-à-dire $Pb=Qa$ .

D’après le théorème de Gauss, cette condition impose $P\mid a.$

Il existe donc $k\in\llbracket0,d\rrbracket$ tel que $a=kP$ , d’où $b=kQ.$

Ainsi : $S_{x}\cap S_{y}=\left\{\left(kP,kQ\right);\thinspace k\in\llbracket0,d\rrbracket\right\}$ et donc $\text{card}\left(S_{x}\cap S_{y}\right)=d+1$ .

Finalement :

$\begin{eqnarray*}& &\text{card}\left(S_{x}\cup S_{y}\right)\\& = & (p+1)+(q+1)-(d+1)\\& = & \boxed{p+q-p\wedge q+1}\end{eqnarray*}$

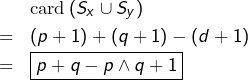
Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse