qr-00004

Question

Pourquoi la fonction exponentielle est-elle égale à sa dérivée ?

Avant de tenter de répondre à cette question, il faut se mettre d’accord sur la manière dont on définit la fonction exponentielle. Car il existe plusieurs définitions (équivalentes entre-elles, fort heureusement) et selon la définition adoptée, il sera plus ou moins aisé de répondre.

Je propose d’envisager deux points de vue, en commençant par le plus rapide et en terminant par celui qui correspond au programme de terminale scientifique (encore que, dans le cadre de ce programme, un argument est admis … et pas des moindres !… cf. ci-dessous).

Réponse 1

Si l’on admet le théorème d’existence de primitives (selon lequel, pour tout intervalle non trivial I\subset\mathbb{R} et pour toute application continue f:I\to\mathbb{R}, il existe F:I\to\mathbb{R} dérivable et telle que F'=f), on peut construire la fonction logarithme népérien en la définissant comme la primitive s’annulant en 1 de l’application continue ]0,+\infty[\to\mathbb{R},\,x\mapsto\frac{1}{x}.

Pour une présentation détaillée du logarithme (construction et preuves des principales propriétés), on pourra consulter cette vidéo.

On constate alors que \ln induit une bijection dérivable de ]0,+\infty[ vers \mathbb{R}, dont la dérivée ne s’annule pas, ce qui entraîne que sa bijection réciproque, appelée par définition « fonction exponentielle » et notée \exp, est aussi dérivable et que :

    \[ \forall x\in]0,+\infty[,\,\exp'(x)=\frac{1}{\ln'(\exp(x))}=\frac{1}{\frac{1}{\exp(x)}}=\exp(x)\qquad\left(\star\right) \]

En outre : \exp(0)=1 puisque \ln(1)=0.

Pour la relation (\star), on s’est appuyé sur le théorème de la bijection dérivable, dont voici l’énoncé.

Si I et J sont des intervalles de \mathbb{R} et et si f:I\to J est une bijection dérivable dont la dérivée ne s’annule pas, alors sa bijection réciproque g=f^{-1} est dérivable et, pour tout y\in J :

    \[ g'(y)=\frac{1}{f'\left(g(y)\right)} \]

Bien entendu, cette première réponse serait plus longue si l’on détaillait la démonstration du théorème d’existence de primitives !

Réponse 2

On considère l’équation différentielle linéaire du premier ordre

    \[ y'=y \]

Si l’on admet qu’il existe une fonction f, dérivable sur \mathbb{R}, et une seule qui est solution de cette équation différentielle et qui vérifie en outre la « condition initiale » f(0)=1, alors le problème est réglé car cette fonction est baptisée « fonction exponentielle » et le fait qu’elle coïncide avec sa dérivée fait partie intégrante de sa définition.

Bien sûr, ce résultat d’existence et d’unicité n’a rien d’évident !

Pour l’unicité, on considère f et g, deux applications dérivables sur \mathbb{R} telles que :

    \[ \forall x\in\mathbb{R},\,f'(x)=f(x)\qquad\textrm{et}\qquad f(0)=1 \]

ainsi que :

    \[ \forall x\in\mathbb{R},\,g'(x)=g(x)\qquad\textrm{et}\qquad g(0)=1 \]

L’idée va être de prouver que g/f est constante et que cette constante vaut 1, mais on ne peut pas envisager cela avant d’avoir prouvé que f ne s’annule pas.

Pour cela, posons pour tout x\in\mathbb{R} : \varphi(x)=f(x)f(-x). Comme f est dérivable, alors \varphi aussi et :

    \[ \forall x\in\mathbb{R},\,\varphi'(x)=f'(x)f(-x)-f(x)f'(-x)=f(x)f(-x)-f(x)f(-x)=0 \]

Il en résulte que \varphi est constante et comme \varphi(0)=f(0)^2=1, alors \forall x\in\mathbb{R},\,f(x)f(-x)=1. En particulier, on voit bien que f ne s’annule pas.

Maintenant, posons pour tout x\in\mathbb{R} : q(x)=g(x)/f(x). Il est clair que q est dérivable (quotient de deux applications dérivables, dont le dénominateur ne s’annule pas) et que :

    \[ \forall x\in\mathbb{R},\,q'(x)=\frac{g'(x)f(x)-g(x)f'(x)}{f(x)^2}=\frac{g(x)f(x)-g(x)f(x)}{f(x)^2}=0 \]

Il est donc établi que q est constante. Comme q(0)=1, on a bien prouvé que f=g.

Pour l’existence, c’est une autre paire de manches (ce qui explique d’ailleurs que ce point soit admis dans le programme de terminale scientifique). On va utiliser des résultats concernant les suites uniformément convergentes d’applications de classe C^1 (notions au programme de deuxième année d’enseignement supérieur scientifique).

On définit une suite (f_n)_{n\in\mathbb{N}} d’applications en posant :

    \[ \forall x\in\mathbb{R},\,f_0(x)=1\qquad\textrm{et}\qquad\forall n\in\mathbb{N},\,\forall x\in\mathbb{R},\,f_{n+1}(x)=1+\int_0^x f_n(t)\,dt \]

Il est facile de voir par récurrence que :

    \[ \forall n\in\mathbb{N},\,\forall x\in\mathbb{R},\,f_n(x)=\sum_{k=0}^n\frac{x^k}{k!} \]

Les f_n sont donc des applications polynomiales (et en particulier, elles sont toutes de classe C^1).

Pour tout segment réel [a,b], en notant M=\max\{\vert a\vert,\,\vert b\vert\}, on voit que :

    \[ \forall n\in\mathbb{N},\,\forall x\in [a,b],\,\vert\frac{x^n}{n!}\vert\leqslant\frac{M^n}{n!} \]

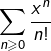or on sait (par la règle de d’Alembert pour les séries numériques à termes strictement positifs) que la série de terme général \displaystyle{\frac{M^n}{n!}} est convergente. Par conséquent, la série d’applications \displaystyle{\sum_{n\geqslant 0}\frac{x^n}{n!}} est normalement (et donc uniformément) convergente sur tout segment. Autrement dit : la suite d’applications (f_n)_{n\in\mathbb{N}} est uniformément convergente sur tout segment. Il en va aussitôt de même de la suite des dérivées, qui est la même (à un décalage près de l’indice) puisque :

    \[ \forall n\in\mathbb{N^\star},\,\forall x\in\mathbb{R},\,f_n'(x)=\frac{d}{dx}\left(\sum_{k=0}^n\frac{x^k}{k!}\right)=\sum_{k=0}^{n-1}\frac{x^k}{k!}=f_{n-1}(x) \]

Notons L la limite simple de la suite (f_n)_{n\in\mathbb{N}}. D’après un théorème classique, L est de classe C^1 sur \mathbb{R} et L'=L. En outre L(0)=\lim_{n\to\infty}f_n(0)=1. On a donc bien montré l’existence d’une fonction dérivable sur \mathbb{R}, qui coïncide en tout point avec sa dérivée et qui prend en 0 la valeur 1.

Partager cet article