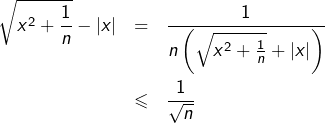Lettre U
UNIFORME (convergence)
Définitions & Vocabulaire
Etant donné un ensemble ![]() considérons :
considérons :
- une suite
 d’applications de
d’applications de  dans
dans 
- une application
- une partie non vide
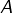 de
de 
➣ On dit que la suite ![]() converge uniformément sur
converge uniformément sur ![]() vers
vers ![]() lorsque :
lorsque :
![]()
![]()
➣ On dit que la suite ![]() converge simplement sur
converge simplement sur ![]() vers
vers ![]() lorsque :
lorsque :
![]()
Il est évident que si ![]() converge uniformément sur
converge uniformément sur ![]() vers
vers ![]() , alors
, alors ![]() converge simplement sur
converge simplement sur ![]() vers
vers ![]() . La réciproque est fausse (voir ci-dessous).
. La réciproque est fausse (voir ci-dessous).
On peut généraliser ces notions en remplaçant ![]() par un
par un ![]() ou
ou ![]() espace vectoriel normé et les modules par des normes.
espace vectoriel normé et les modules par des normes.
On peut essayer d’interpréter géométriquement la notion de convergence uniforme :
Illustration dynamique
On a représenté en rouge le graphe de :
![]()
Le graphe de ![]() apparaît en bleu.
apparaît en bleu.
Le fuseau limité par les graphes de ![]() et de
et de ![]() est représenté en vert.
est représenté en vert.
La droite d’équation ![]() est dessinée en pointillés.
est dessinée en pointillés.
Les trois sliders permettent de choisir les valeurs de ![]() de
de ![]() et de
et de ![]()
Pour ![]() et pour
et pour ![]() fixé, on constate que, dès que
fixé, on constate que, dès que ![]() est assez grand, le graphe de
est assez grand, le graphe de ![]() est entièrement compris dans le fuseau limité par les graphes de
est entièrement compris dans le fuseau limité par les graphes de ![]() et de
et de ![]() Ceci illustre le fait que la suite
Ceci illustre le fait que la suite ![]() converge uniformément vers
converge uniformément vers ![]()
Si ![]() la suite de terme général
la suite de terme général
![]()
En pratique, pour établir la convergence uniforme de ![]() vers
vers ![]() sur
sur ![]() il suffit de majorer (pour tout
il suffit de majorer (pour tout ![]() l’écart
l’écart ![]() par une quantité indépendante de
par une quantité indépendante de ![]() et qui tend vers 0 lorsque
et qui tend vers 0 lorsque ![]()
Exemple
La suite d’applications
![]()
![]()
![]()

La convergence simple n’implique pas la convergence uniforme.
Exemple
La suite d’applications
![]()
![Rendered by QuickLaTeX.com \[\sup_{x\in\left[0,1\right]}nx^{n}\left(1-x\right)=\left(\frac{n}{n+1}\right)^{n+1}\rightarrow\frac{1}{e}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-23775214666bd123b148945cc9d6cdc3_l3.png)
Supposons désormais que ![]() soit un intervalle de
soit un intervalle de ![]() (de longueur non nulle) et que
(de longueur non nulle) et que ![]() soit une suite d’applications de
soit une suite d’applications de ![]() dans
dans ![]() qui converge simplement sur
qui converge simplement sur ![]() vers
vers ![]()
Si les ![]() partagent une propriété commune, il est naturel de chercher à savoir si cette propriété est aussi vérifiée par
partagent une propriété commune, il est naturel de chercher à savoir si cette propriété est aussi vérifiée par ![]() C’est le cas pour :
C’est le cas pour :
- la positivité,
- la croissance,
- la convexité.
Ce n’est pas le cas – en général – pour :
- le caractère bornée,
- la continuité en
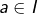 donné, la continuité tout court,
donné, la continuité tout court, - l’uniforme continuité.
Mais si la convergence est uniforme, alors ![]() hérite de chacune des trois propriétés ci-dessus. En outre, on peut citer le :
hérite de chacune des trois propriétés ci-dessus. En outre, on peut citer le :
Théorème
si ![]() est un segment
est un segment ![]() si chaque
si chaque ![]() est continue et si la suite
est continue et si la suite ![]() converge uniformément vers
converge uniformément vers ![]() alors (
alors (![]() est continue et) :
est continue et) :
![]()
Il existe aussi des propriétés qui ne passent pas à la limite uniforme. C’est le cas de la dérivabilité en un point donné de l’intervalle ![]()
Exemple
Pour tout ![]() l’application
l’application
![]()
La suite ![]() converge uniformément sur
converge uniformément sur ![]() vers
vers ![]() qui n’est pas dérivable en
qui n’est pas dérivable en ![]() bien que chaque
bien que chaque ![]() le soit (pour tout
le soit (pour tout ![]()
![]() est dérivable et même de classe
est dérivable et même de classe ![]()
La convergence uniforme est justifiée par le fait que, pour tout ![]() et pour tout
et pour tout ![]() :
: