Lettre O
ORDRE (relation d’)
Etant donné un ensemble ![]() une relation binaire
une relation binaire ![]() sur
sur ![]() est appelée une relation d’ordre lorsqu’elle est :
est appelée une relation d’ordre lorsqu’elle est :
- réflexive :
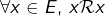
- antisymétrique :
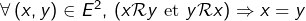
- transitive :
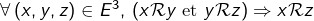
Quelques exemples classiques :
- la relation
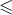 (inférieur ou égal ) dans
(inférieur ou égal ) dans 
- l’ordre lexicographique associé à un alphabet
- la relation ⊂ (inclusion) dans
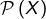 où
où  est un ensemble quelconque
est un ensemble quelconque - la relation | (divisibilité) dans
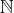
D’une manière générale, étant donnée une relation d’ordre ![]() sur un ensemble
sur un ensemble ![]() l’ordre est dit total lorsque les éléments de
l’ordre est dit total lorsque les éléments de ![]() sont deux à deux comparables :
sont deux à deux comparables :
![]()
Etant donné un ensemble ![]() muni d’une relation d’ordre
muni d’une relation d’ordre ![]() une partie
une partie ![]() de
de ![]() possède un plus petit élément lorsque :
possède un plus petit élément lorsque :
![]()
L’ensemble ![]() est dit bien ordonné lorsque toute partie non vide de
est dit bien ordonné lorsque toute partie non vide de ![]() admet un plus petit élément.
admet un plus petit élément. ![]() est donc bien ordonné alors que
est donc bien ordonné alors que ![]() ne l’est pas (pour l’ordre usuel
ne l’est pas (pour l’ordre usuel ![]() Noter qu’un bon ordre est nécessairement un ordre total : étant donnés
Noter qu’un bon ordre est nécessairement un ordre total : étant donnés ![]() ces deux éléments sont comparables puisque la paire
ces deux éléments sont comparables puisque la paire ![]() admet un plus petit élément.
admet un plus petit élément.
Une conséquence de l’axiome du choix est l’existence, pour tout ensemble non vide, d’un bon ordre.
ORTHOCENTRE
Etant donné une triangle ![]() du plan affine euclidien, on définit la hauteur issue de
du plan affine euclidien, on définit la hauteur issue de ![]() comme étant la droite passant par le sommet
comme étant la droite passant par le sommet ![]() et perpendiculaire à la droite
et perpendiculaire à la droite ![]()
On définit pareillement les hauteurs issues de ![]() et de
et de ![]()
Comme le suggère l’illustration dynamique ci-dessous, les trois hauteurs d’un triangle sont concourantes : elles passent toutes les trois par un même point, appelé orthocentre de ![]()
Illustration dynamique
Mode d’emploi
Lorsqu’on déplace le curseur, le sommet le plus proche est activé (si toutefois il est assez proche). En pressant simultanément sur SHIFT, on déplace ce point.
Sous la figure, sont disposés 5 boutons :
- Bouton H : active / désactive l’affichage des hauteurs et de l’orthocentre H
- Bouton G : active / désactive l’affichage de l’isobarycentre G
- Bouton O : active / désactive l’affichage du cercle circonscrit et de son centre O
- Bouton E : active / désactive l’affichage de la droite d’Euler, du cercle d’Euler et de son centre E
- Bouton 9 : active / désactive l’affichage des neufs points d’Euler (à savoir : les milieux des côtés, les pieds des hauteurs et les milieux des segments joignant chaque sommet à l’orthocentre). Ces 9 points sont cocycliques : le cercle qui les porte est appelé cercle d’Euler du triangle.
Voici comment prouver que les trois hauteurs sont concourantes.
Les hauteurs issues de ![]() et de
et de ![]() sont sécantes en un point
sont sécantes en un point ![]() (elles ne sont pas paralèlles, sans quoi les droites
(elles ne sont pas paralèlles, sans quoi les droites ![]() et
et ![]() seraient parallèles, donc confondues et
seraient parallèles, donc confondues et ![]() ne serait pas un vrai triangle …). Il s’agit de voir que
ne serait pas un vrai triangle …). Il s’agit de voir que ![]() appartient à la hauteur issue de
appartient à la hauteur issue de ![]() Pour cela, on s’appuie sur la relation :
Pour cela, on s’appuie sur la relation :
(![]() )
) ![]()
Choisissons ![]() . Par hypothèse, les produits scalaires
. Par hypothèse, les produits scalaires ![]() et
et ![]() sont nuls. Il en résulte que
sont nuls. Il en résulte que ![]() ce qui prouve que
ce qui prouve que ![]() appartient à la hauteur issue de
appartient à la hauteur issue de ![]()
Preuve de la relation 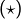 (cliquer pour déplier / replier)
(cliquer pour déplier / replier)
D’après la relation de Chasles :
![]()
![]()
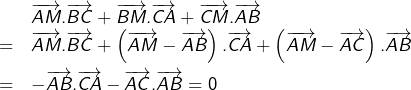
OSCILLANTE (suite)
Une suite réelle ![]() est dite oscillante lorsque son sens de variation est « en zig-zag » : une alternance de montées et de descentes …
est dite oscillante lorsque son sens de variation est « en zig-zag » : une alternance de montées et de descentes …
De manière précise, cela signifie que l’expression ![]() est de signe constant.
est de signe constant.
Si ce signe est positif, alors :
![]()
![]()
Exemple 1
La suite de terme général ![]() est oscillante.
est oscillante.
Exemple 2
Si ![]() alors la suite définie par :
alors la suite définie par :
![]()
Plus généralement, si ![]() est un intervalle (non trivial) de
est un intervalle (non trivial) de ![]() et si
et si ![]() est décroissante, alors pour tout
est décroissante, alors pour tout ![]() la suite définie par les relations :
la suite définie par les relations :
![]()
Remarque
On notera que si ![]() est oscillante, alors les suites extraites
est oscillante, alors les suites extraites ![]() et
et ![]() sont monotones et de sens de variation contraires. Dans certains cas, on peut montrer avec le théorème de la limite monotone que ces deux suites convergent vers une même limite
sont monotones et de sens de variation contraires. Dans certains cas, on peut montrer avec le théorème de la limite monotone que ces deux suites convergent vers une même limite ![]()
On peut alors conclure que la suite ![]() converge vers
converge vers ![]()
OUVERT
La notion de partie ouverte est présentée ici dans ![]() par souci de simplicité. Son cadre naturel est celui des espaces topologiques.
par souci de simplicité. Son cadre naturel est celui des espaces topologiques.
On dit d’une partie ![]() de
de ![]() que c’est un ouvert lorsque :
que c’est un ouvert lorsque :
![]()
Les parties suivantes de ![]() sont des ouverts :
sont des ouverts :
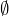

![Rendered by QuickLaTeX.com \left]a,b\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-d1d94c9271a36378aed6d48018b45fab_l3.png) pour tout couple
pour tout couple 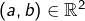 tel que
tel que 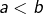
- l’union de toute famille d’ouverts
- l’intersection d’une famille finie d’ouverts
- l’image réciproque d’un ouvert par une application continue
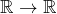
Les parties suivantes de ![]() ne sont pas des ouverts :
ne sont pas des ouverts :
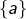 pour tout
pour tout 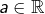
![Rendered by QuickLaTeX.com \left[a,b\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-358a945a8ec946c0449cbd1d69dc7a36_l3.png)
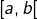 et
et ![Rendered by QuickLaTeX.com \left]a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0f2c15019bfab09ca8d076c11ab19509_l3.png) pour tout couple
pour tout couple 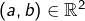 tel que
tel que 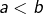
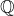 et
et 

