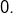On peut écrire 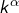 sous la forme
sous la forme 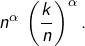
On peut écrire 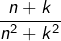 sous la forme
sous la forme 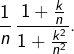
La somme 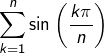 peut être vue comme la partie imaginaire de
peut être vue comme la partie imaginaire de 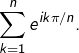
L’inégalité de Jensen « discrète » permet d’écrire une inégalité entre sommes de Riemann. On passe ensuite à la limite dans cette inégalité.
Appliquer la formule de Taylor-Lagrange à l’ordre 2 à 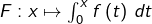 sur le segment
sur le segment ![Rendered by QuickLaTeX.com \left[\dfrac{k-1}{n},\dfrac{k}{n}\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-859cfb2ad31a52c74ad9fc9c357174cf_l3.png)
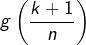 n’est pas très éloigné de
n’est pas très éloigné de 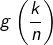 … On devine que la limite demandée doit être
… On devine que la limite demandée doit être 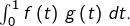
On peut commencer par écrire :
![Rendered by QuickLaTeX.com \[\dfrac{k}{n}=\left(1-\dfrac{k}{n}\right)\dfrac{k}{n+1}+\dfrac{k}{n}\thinspace\dfrac{k+1}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-78322ce40bd70fdbe2b574a86c537407_l3.png)
puis invoquer la convexité de
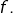
Lorsque  est grand, on imagine que sur la plupart des intervalles
est grand, on imagine que sur la plupart des intervalles ![Rendered by QuickLaTeX.com \left[x_{k,n},\thinspace x_{k+1,n}\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-dcd83201b293056be2a3680a392df275_l3.png) la fonction
la fonction  n’a guère le temps de changer de signe. Si tel est le cas :
n’a guère le temps de changer de signe. Si tel est le cas :
![Rendered by QuickLaTeX.com \[\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|=\int_{x_{k,n}}^{x_{k+1,n}}\left|f\left(t\right)\right|\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa37de5155456131167bf60927511c56_l3.png)
Changer de variable pour montrer la convergence de l’intégrale 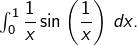 Ensuite, pour montrer la divergence de la suite
Ensuite, pour montrer la divergence de la suite 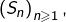 on peut essayer de montrer que la suite
on peut essayer de montrer que la suite 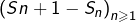 ne converge pas vers
ne converge pas vers