

➡ Pour ![]() : trouver un équivalent en 0 et calculer la limite en 1.
: trouver un équivalent en 0 et calculer la limite en 1.
➡ Pour ![]() : montrer la convergence absolue.
: montrer la convergence absolue.
➡ Pour ![]() : trouver des équivalents en 0 et en 1.
: trouver des équivalents en 0 et en 1.
➡ Pour ![]() : réviser la nature de l’intégrale (dite de Dirichlet)
: réviser la nature de l’intégrale (dite de Dirichlet) ![]() puis linéariser
puis linéariser ![]()
➡ Pour ![]() : la fonction est prolongeable par continuité en 0. En
: la fonction est prolongeable par continuité en 0. En ![]() la règle des équivalents n’est pas applicable, mais on peut effectuer un développement asymptotique.
la règle des équivalents n’est pas applicable, mais on peut effectuer un développement asymptotique.
➡ Pour ![]() : trouver un équivalent en
: trouver un équivalent en ![]() après avoir factorisé le polynôme
après avoir factorisé le polynôme ![]()

Raisonner par l’absurde.
Si par exemple ![]() admettait en
admettait en ![]() une limite
une limite ![]() quelle serait alors la limite de l’intégrale partielle
quelle serait alors la limite de l’intégrale partielle ![]() lorsque
lorsque ![]() ?
?

Intégrer par parties et raisonner par récurrence.

Comme ![]() l’application
l’application ![]() est continue. Dans les cas où
est continue. Dans les cas où ![]() la comparer à une fonction du type
la comparer à une fonction du type ![]() au voisinage de
au voisinage de ![]() Dans le cas
Dans le cas ![]() effectuer une comparaison avec l’intégrale de
effectuer une comparaison avec l’intégrale de ![]()

On peut deviner la limite de la suite ![]() en dessinant la forme de la courbe de la fonction
en dessinant la forme de la courbe de la fonction ![]() pour
pour ![]() grand.
grand.
Pour montrer que ![]() un simple encadrement de
un simple encadrement de ![]() devrait faire l’affaire.
devrait faire l’affaire.
Enfin, pour déterminer la nature de la série de terme général ![]() , je vous suggère d’établir une inégalité et d’appliquer le principe de comparaison … mais c’est à vous de décider s’il faut chercher à majorer ou bien à minorer
, je vous suggère d’établir une inégalité et d’appliquer le principe de comparaison … mais c’est à vous de décider s’il faut chercher à majorer ou bien à minorer ![]() 😉
😉

La majoration classique ![]() est la clef pour établir l’encadrement demandé.
est la clef pour établir l’encadrement demandé.
Ensuite, le changement de variable ![]() dans l’intégrale
dans l’intégrale ![]() fait apparaître une intégrale de Wallis.
fait apparaître une intégrale de Wallis.
Il reste à trouver un « bon » changement de variable pour l’autre intégrale.

L’idée sous-jacente est très géométrique !
Observer que l’intégrale partielle ![]() est égale à la somme partielle
est égale à la somme partielle 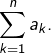
Ceci montre l’existence d’une limite finie pour ![]() lorsque l’entier
lorsque l’entier ![]() tend vers
tend vers ![]()
Il restera à trouver comment faire pour en dire autant de ![]() lorsque le réel
lorsque le réel ![]() tend vers
tend vers ![]() .
.
Enfin, pour montrer que ![]() n’admet pas de limite en
n’admet pas de limite en ![]() penser à la caractérisation séquentielle de la limite …
penser à la caractérisation séquentielle de la limite …

Le théorème de dérivation sous le signe ![]() donne immédiatement la positivité de
donne immédiatement la positivité de ![]() On peut aussi (plus élémentaire) revenir à la définition de la convexité et montrer que :
On peut aussi (plus élémentaire) revenir à la définition de la convexité et montrer que :
![]()
Observer que l’on peut écrire :
![]()
Ensuite, il s’agit de montrer que ![]() Dériver sous le signe
Dériver sous le signe ![]() et penser à l’inégalité de Cauchy-Schwarz.
et penser à l’inégalité de Cauchy-Schwarz.

Notons ![]() le graphe de
le graphe de ![]() Pour tout
Pour tout ![]() et pour tout
et pour tout ![]() comparer les pentes des trois cordes dont les extrémités sont :
comparer les pentes des trois cordes dont les extrémités sont :
- les points d’abscisses
 et
et 
- les points d’abscisses
 et
et 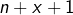
- les points d’abscisses
 et
et 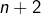
Utiliser l’encadrement obtenu pour montrer que :
![]()
